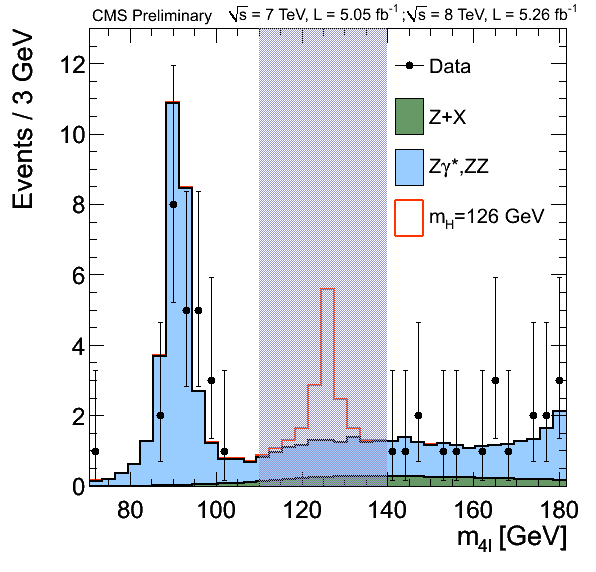
CMS performs searches for new particles by looking for signals amidst a background of known physics. If the data begin to indicate something more interesting than merely background - for instance, more decay events than expected in a certain region - it is important to make sure that the observation is statistically significant by collecting and analysing more data. However, we don't want to bias our analyses by optimising the analysis based on what was already seen. To avoid such bias while analysing new data, physicists draw "blinds” over the region where an excess of decay events is expected; this region is only "unblinded" when they are satisfied with their procedures. This ensures objectivity when it comes to looking for much-sought-after signs of new physics, and gives confidence in the ultimate result.

The procedure is similar to that used by medical researchers when testing a new treatment. Even though the Higgs boson was discovered a decade ago, we still employ this procedure for measuring the Higgs boson's properties - we still do not want to bias these measurements by optimising towards deviations from the standard model expectations! All of the available data, including those in the blinded region, are used in the analysis; you just don’t peek at this region to see how it changes as you tweak various selection criteria. In many of the on-going searches and measurements, data corresponding to a possible signal look very similar to data corresponding to background.

Therefore, once the analysis is blinded, physicists must optimise two things: 1) simulations, to help determine the criteria for selecting signals and 2) the methods for rejecting or quantifying background events using data from the region where there is no excess. To cross-check all the details, the various steps involved in the analysis procedures are usually carried out by at least two independent teams. If both teams see similar results in the background region, the analysis is signed off by the wider collaboration. It is only after the sign-off that the signal region is unblinded. The results of the unblinding are put through further scrutiny by the collaboration before being made public.

A dangerous beast is hiding in today’s searches for the rare signs of new physics — or even “old” physics, such as the Higgs boson — at the Large Hadron Collider. It is called “Look-Elsewhere Effect”, LEE for insiders. What is it, and why should you care? Imagine you look for a heavy particle decaying into a pair of hadronic jets: a commonplace test case in high-energy physics. You have your background model, which predicts the observable shape of the di-jet mass distribution, and you know what kind of a bump a new particle signal would produce in that shape. So you search for such a bump in the data, but — not knowing where it might appear — you search everywhere. You have worked all day, and the night is nearing; you prepare yourself a martini and spin your analysis program. To your amazement, the program finds a significant bump at some particular mass value: is it a real signal? To claim it is a new signal, the effect must reach or exceed the “five-sigma” significance level, five standard deviations away from the expectation: that's a rather silly but well-established rule. But if yours gives only 3.5 or four sigma, are you allowed to get excited and wake up your boss, or should you sit back and sip your martini, with an “I know better” grin on your face? I claim the latter is a better option. You have fallen prey to the LEE: you looked in many places for a possible signal, and found a significant effect somewhere; the likelihood of finding something in the entire region you probed is greater than it would be if you had stated beforehand where the signal would be, because of the “probability boost” of looking in many places. A good rule of thumb is the following: if your signal has a width W, and if you examined a spectrum spanning a mass range from M1 to M2, then the “boost factor” due to the LEE is (M2-M1)/W. This may easily amount to a factor of 10 or 100, depending on the details of your search. An effect occurring by chance once in ten thousand cases in a given place on your spectrum may actually be just an unexciting one-in-a-hundred fluctuation! In fact, the “five-sigma” rule I mentioned above was conceived with exactly this particular effect in mind. Five sigma is a really, really rare occurrence (three in ten million), so even including the LEE, it is still something to take quite seriously. Now-a-days, we publish three-sigma results that may or may not go away with more data, and our scientific integrity requires us to account for the LEE. This is actually less easy to do than by just multiplying a probability by (M2-M1)/W as in the example above: in complex searches such as that for the Higgs boson, which combine bump hunts in many channels, this is not a trivial task. A recent paper by E. Gross and O. Vitells (Eur. Phys. J. C70:525-530,2010) has clarified some of the technical issues. The searches for the Higgs boson by CMS and ATLAS are sizing up the LEE by studying the probability of the background-only hypothesis as a function of the Higgs mass: the more the observed p-value distribution varies up and down as the signal mass hypothesis change, the stronger is the Look-Elsewhere-Effect correction that is required. Stuff for experts, for sure. But outsiders have better be aware that a three-sigma effect should not be blindly dubbed “evidence” for something new in the data. As travellers to a foreign country whose tax habits are unknown, you better ask before you buy, “LEE included or not”? — Submitted by Tommaso Dorigo