What if new particles modify the behaviour of existing particles, but by only a little bit? In a new result, CMS physicists search for new physics using a technique called Effective Field Theory to study the top quark in a "toy universe".
We have many good reasons to believe that we have yet to discover all of the particles in nature. For example, dark matter seems to be a new type of particle we haven’t produced in the laboratory yet. A primary goal of the LHC is to produce and then study these undiscovered particles by colliding protons together at the highest energies ever achieved by human ingenuity. High collision energy is vital because the most likely reason for a particle to remain undiscovered today is that it is too massive to have been produced in previous, lower energy, experiments. The high energy of the LHC is letting us explore particle mass scales that were never previously accessible. This is a triumph of human creativity, determination, and collaboration, and an inspiring scientific opportunity.
But what if the new particles we seek are so massive they remain beyond the energy reach of even the LHC? This would undoubtedly be a disappointment, but it turns out that with a little cleverness and perseverance, we could still learn something from the LHC data about new particles even if they’re too massive to make at the LHC. Even undiscovered particles can influence the outcomes of proton collisions by participating in them virtually. Having virtual particles in a collision is like borrowing particles from the universe for a short time so that you can have some very rare type of proton collision occur. The virtual particle has to be “paid back” to the universe, so it can’t appear among the particles that emerge from the collision, but it can still have an impact on what happens during the collision. The challenge is that the effects of virtual particles are very subtle, so detecting new particles this way requires both precise measurements and detailed theoretical predictions.
There are a vast number of diverse theoretical predictions that describe new massive particles that could exist. Without knowing more about what we’re looking for, it seems like there would be too many different scenarios to make precise theoretical predictions of what to expect, and to test all these scenarios with dedicated experimental studies. However, there is a trick that makes our job in predicting what to expect in our data much easier. Even though we don’t know anything about the new particle or particles, we know that adding them to the theory can’t disrupt the desirable features of our current theory. So, the new contributions can’t spoil physics principles like translational or rotational invariance (that is, our answer can’t depend on where in space you make your measurement or how you orient your perspective). When we account for all the known symmetries of nature, it turns out that there are only 59 distinct ways (keeping only the most essential contributions) that new particles could impact any measurement we’d make. Any new theory will just boil down to some combination of different amounts of these 59 different effects. This approach is known as effective field theory, and it gives us a powerful new tool to look for signs of new physics. Effective field theory essentially provides us with a toy universe with 59 knobs that we can turn to try to match whatever we see in the data.
The CMS experiment collects a massive amount of data that can be used to make many different measurements. To make progress, we need to decide where to apply our effective field theory techniques to look for signs of something new. One exciting corner of the data to peer into is collisions that produce top quarks along with other particles. The top quark is the most massive particle we’ve catalogued so far, making it historically very difficult to produce and study. The LHC is the first accelerator capable of producing enough top quarks to allow us to study them in great detail. As we look more closely, there are still plenty of opportunities to see something surprising in the data!
Top quarks are not stable particles; a top quark decays immediately into two other particles, a W boson and another type of quark, the bottom quark. W bosons are also not stable. They decay in different ways. Sometimes they decay into a charged lepton, like an electron or muon, and a neutrino. The CMS detector is designed to directly detect electrons and muons with high precision. Other times they decay into quarks. Quarks, like the bottom quark or the quarks from a W boson, turn into collimated sprays of particles, called jets. Looking for collisions that produce a mixture of electrons and/or muons plus jets is a good way to identify ones in which top quarks were produced.
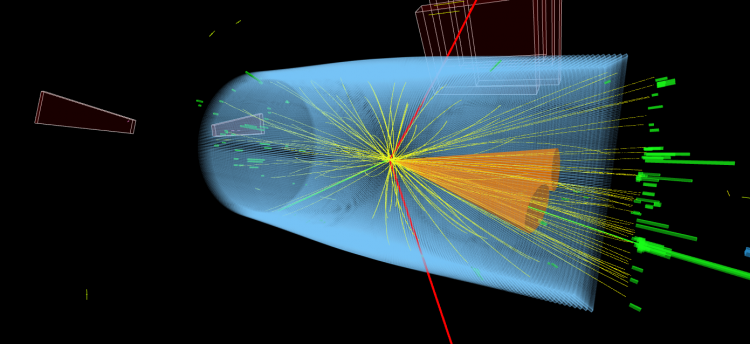
But wait, we want to find collisions where not just top quarks are produced but also other particles, like extra W bosons, Z bosons, or even Higgs bosons. Well, since these extra particles are also not stable, the trick comes down to looking for the particle that they decay into. All of these particles have ways to decay that involve leptons, so looking for events that have extra leptons is an excellent way to spot collisions that produced more than just top quarks. For example, a top quark collision shouldn’t be able to produce more than two charged leptons, so a collision like the one in Figure 1 is a likely candidate to be a collision in which more than just top quarks but also extra particles like a W, Z or Higgs boson were also produced.
Figure 1: A collision with three leptons. The orange cones represent the four jets arising from quarks or gluons. The red lines show the paths of two muons. The green line shows the path of an electron. There is a second electron inside one of the jets, likely originating from a bottom quark decay. There are too many leptons in this collision to have come from just the production of two top quarks.
So now we have the recipe for our measurement: First, count the number of collisions recorded by the CMS detector that have too many charged leptons. Next use effective field theory to calculate how many collisions with different numbers of leptons we would expect to see, depending on the “settings” of the different “knobs.” For making collisions involving top quarks and extra particles, it turns out that only 16 of the 59 knobs have a really strong impact on the outcome, so we focus on those. Then we try turning those 16 knobs to see which settings produce predicted collision counts that best agree with those we observe. Figure 2 shows an animated example of this process in action.
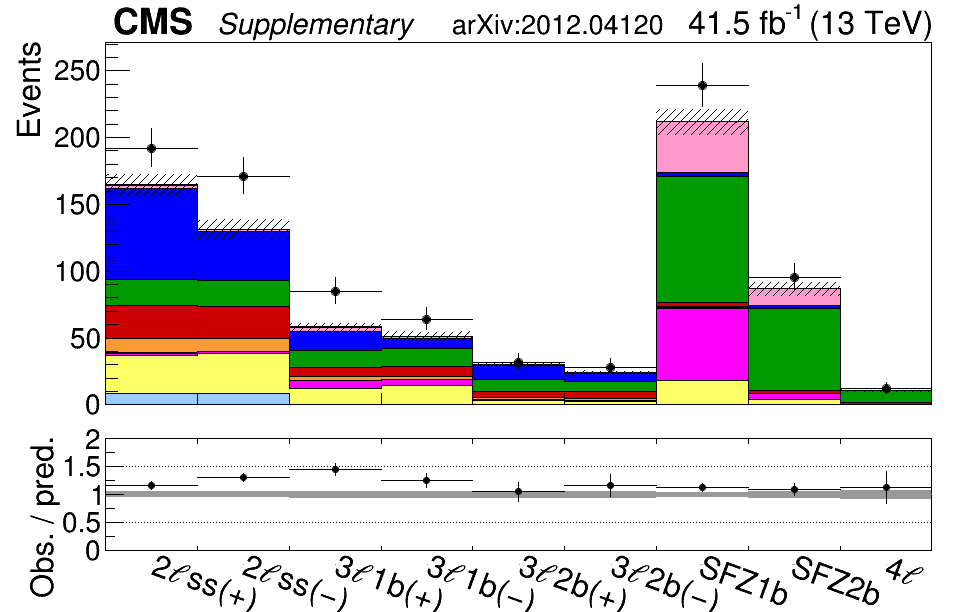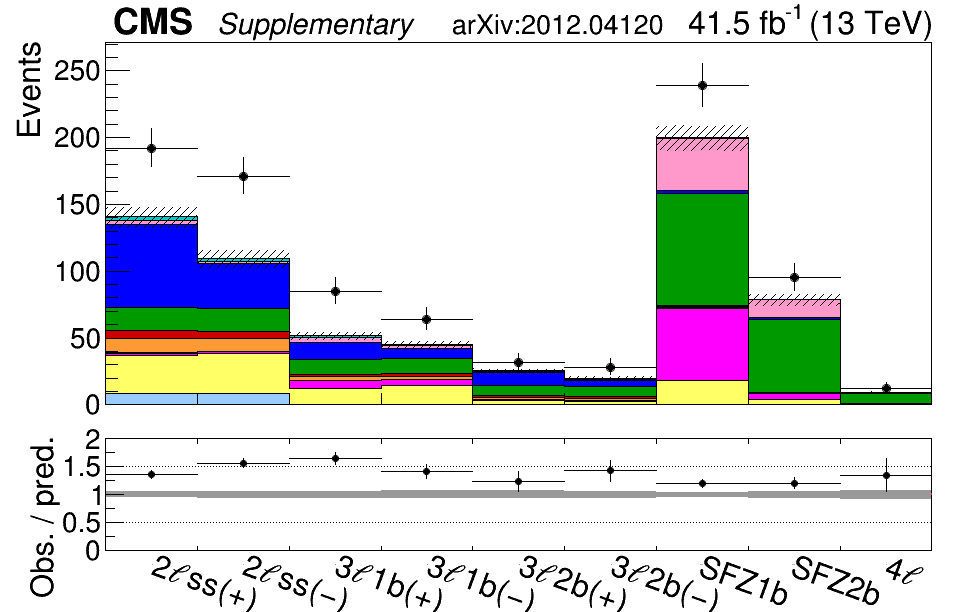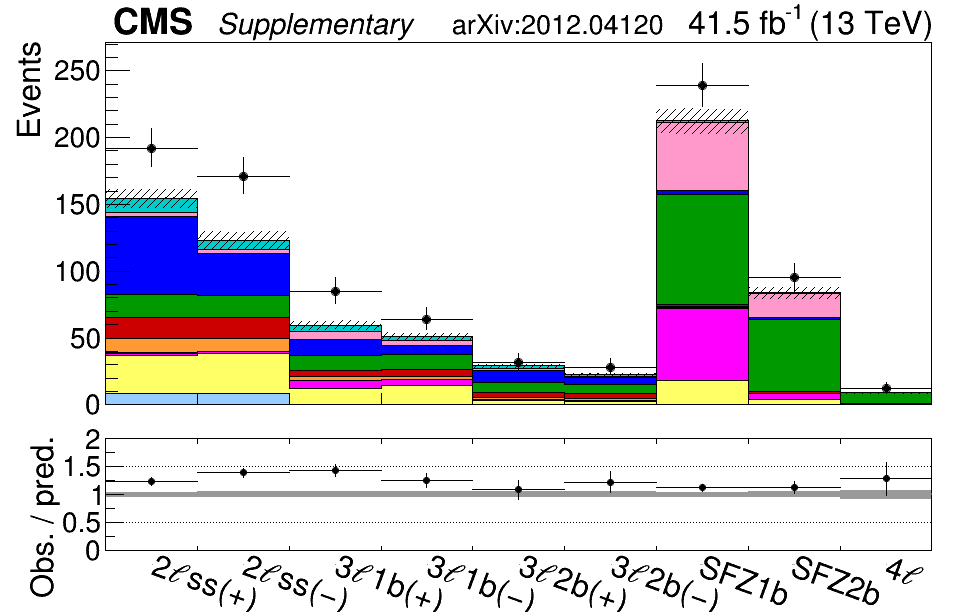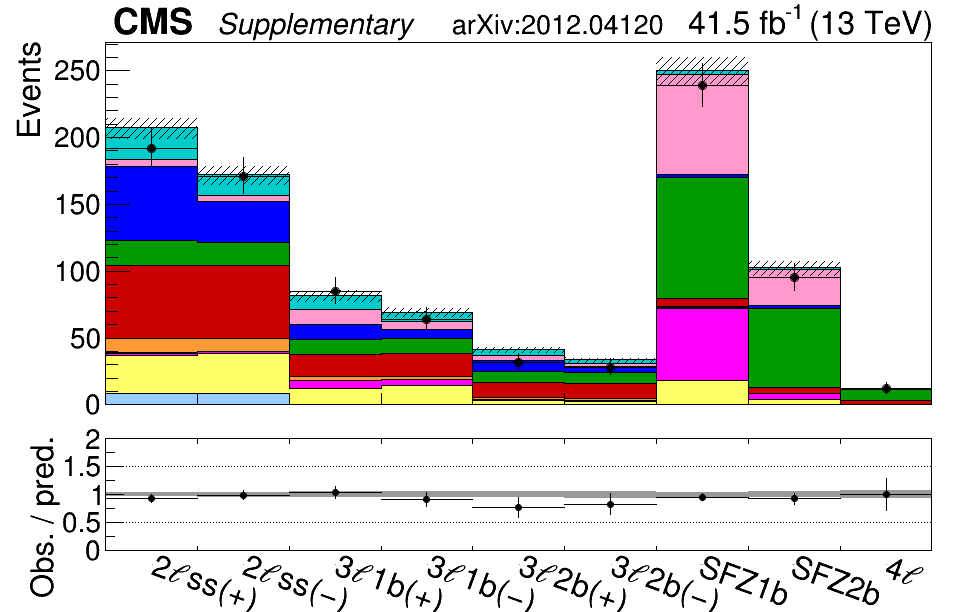
Figure 2: A plot of the number of collisions in the CMS data that have more leptons than you’d expect for top quark production. The y-axis shows the count of collisions, also called events. At the same time, the x-axis divides the data into different distinct categories depending on the number of leptons as well as the number of bottom quark jets detected. As we turn the knobs of the effective field theory, the number of predicted events, shown as the colored bars, moves up and down. Settings of the knobs that produce predictions that most closely match the data (black points with error bars) represent theories that are worth studying more closely. In contrast, settings that predict something very different from what we observe can be discarded from further consideration.
We don’t have enough precision in our data to pin down the exact knob settings of the effective field theory that best reflect reality. Uncertainties in our measurements come from both the precision of our detectors and the amount of data we’ve collected. These uncertainties mean we can only restrict each knob to a range of possible values, but knowing this range is extremely interesting! The settings of the effective field theory knobs represent different possible theories with new particles that are too heavy to detect directly at the LHC. By figuring out which settings are consistent with the data, we’re figuring out which theories might be correct and which ones are ruled out by the data. Figure 3 shows an example of a plot indicating which knob settings best match the data. Values inside the ellipses are more consistent with the data, while values outside are less consistent. The diamond marker at the center of the plot corresponds to setting the knobs to zero, which means no new particles added to the theory. Since that knob setting is inside the ellipse, that possibility is not yet ruled out by the data. As CMS records more data, and we develop and employ more powerful analysis techniques, the goal is to shrink the size of the ellipse. Measuring more accurately will allow physicists to check if the diamond at the center of the plot will stay inside the ellipse, meaning maybe there are no new particles or move outside, which would mean we need some new particles to explain that data!
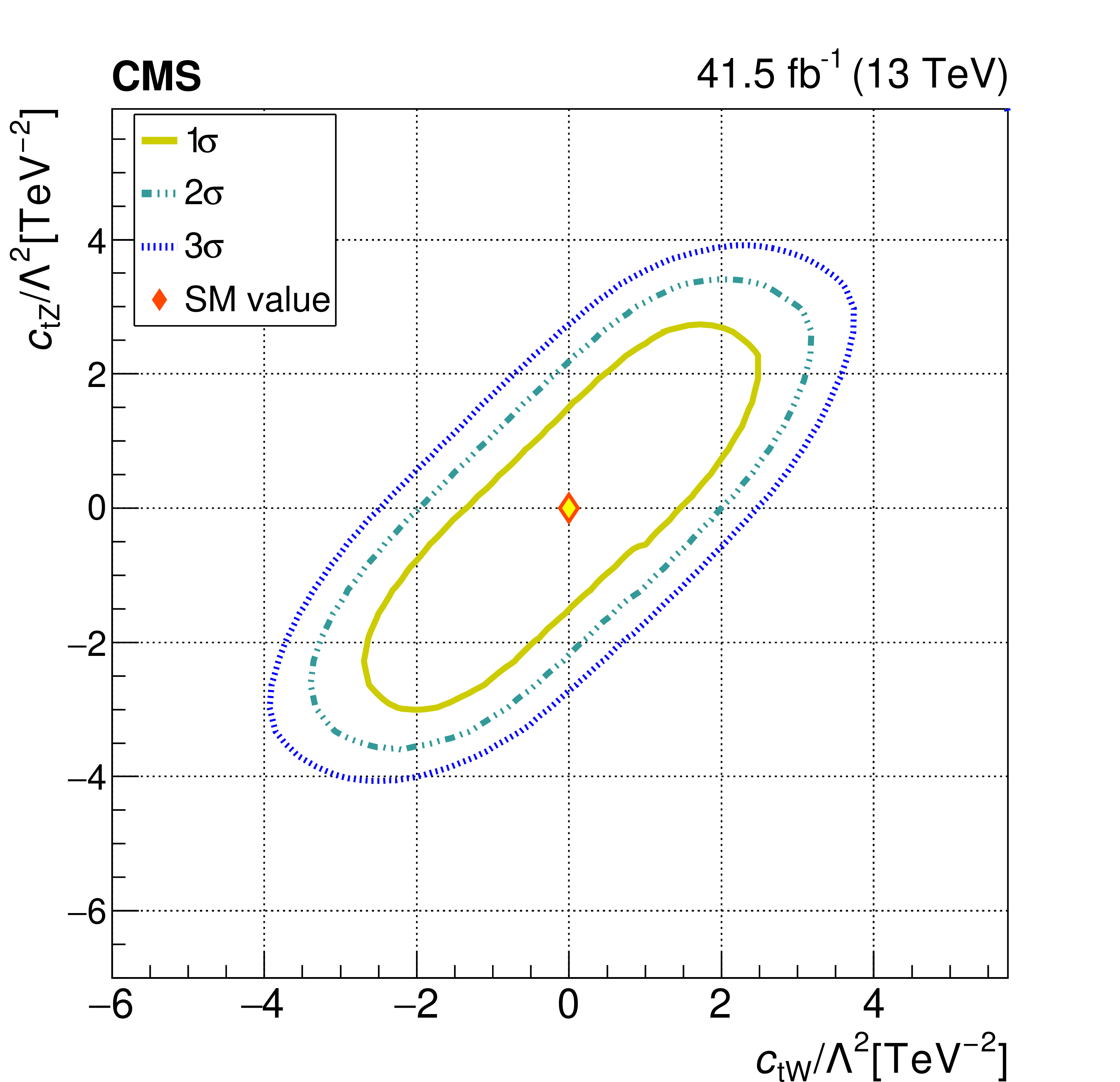
Figure 3: A plot showing which effective field theory knob settings are most consistent with data. The x- and y-axes show possible knob settings. The values of zero at the center of the plot, represented by the diamond marker, indicate knob settings with no new particles. The three curves on the plot show the region which is most consistent with the data. The three curves just differ in how confident we are that the value inside is still allowed by the data. We are most confident that the values inside the inner curve are consistent with the data but less confident about the values inside the larger ellipses.

