A new result by the CMS collaboration accepted by the journal Physical Review Letters demonstrates for the first time that top quarks are produced in nucleus-nucleus collisions. At the same time, this also demonstrates the capability of the CMS experiment to perform top quark studies in this unusual and challenging environment, something that very few people would have betted on until a few years ago.
To provide the context for this breakthrough, let us recall that the flagship accelerator of CERN is named the Large Hadron Collider (LHC) and not the Large Proton Collider. This is despite how the LHC’s record-energy proton-proton collisions brought the discovery of the Higgs boson, and a vast program of searches for physics beyond the Standard Model. In a typical year of LHC operation, one out of seven months of collisions is devoted to heavy-ion beams. While proton-proton collisions are, for example, used to precisely pin down the properties of the Higgs boson and the top quark, heavy-ion collisions are used to investigate strongly-interacting matter at extreme energy densities. In particular, they are used to study quark-gluon plasma, an extreme state of matter that filled the Universe in its first microseconds of life. Studies into quark-gluon plasma are the realm of ALICE, a dedicated experiment at the LHC. However, unlike CMS or ATLAS, ALICE was never expected to be able to select top quarks.
With a mass at around 170 times that of the proton, the top (t) quark is the heaviest known elementary particle (see Figure 1). It is also a unique and potentially very powerful tool to understand the inner content of nuclear matter.
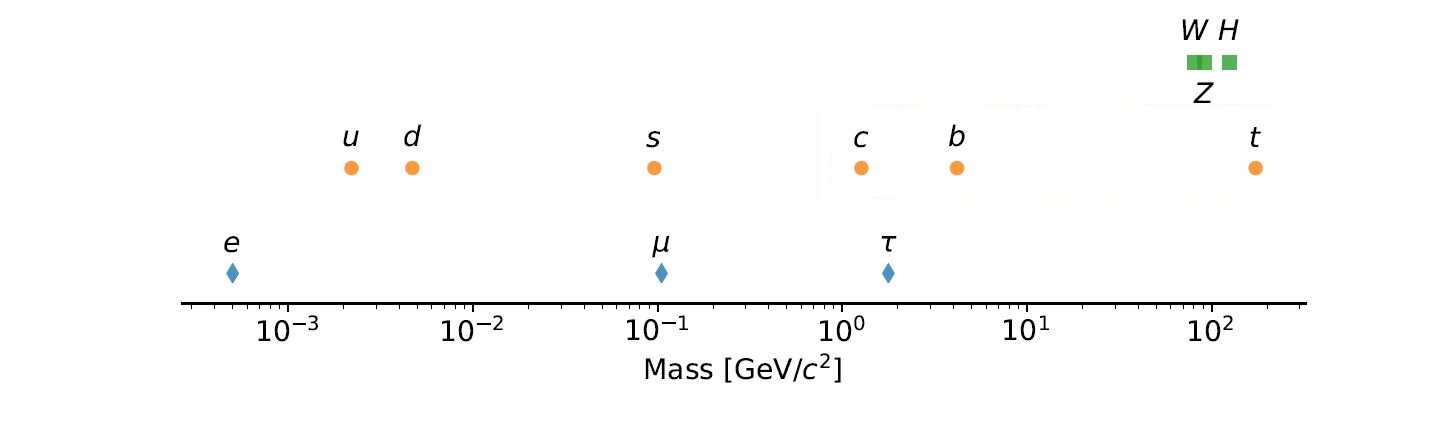
Figure 1: Masses of the massive vector and scalar bosons (green squares), quarks (orange circles), and charged leptons (blue diamonds). This figure includes all the elementary particles whose masses have been measured to be non zero.
The creation of a particle-antiparticle pair of such a massive quark requires for a large amount of kinetic energy to be converted into mass through a single, elementary interaction. Quarks (q) and gluons (g) inside protons and neutrons have a very large spread in energy. Therefore, only a tiny fraction of their collisions pass the threshold energy required for top quark production to occur. This means that, by selecting events containing top quarks, one is implicitly studying only the most energetic elementary collisions. As a consequence of the Heisenberg principle, these collisions probe the smallest space-time distances.
The top quark’s large mass also results in it decaying faster than any other known quark. While the average lifetime of a top quark is of the order of a yoctosecond (0.000000000000000000000001 s or 10-24 s), the lifetime of its sibling, the bottom (b) quark, is of the order of a picosecond (10-12 s). This matters because a yoctosecond is still hundreds of times shorter than the time required for quantum chromodynamic (QCD) processes to take place. These QCD processes include hadronisation, which “dresses” all other quarks until the final state only contains colour-neutral particles, where colour is the QCD equivalent of charge. Additional examples are the formation, expansion and cooling of the quark-gluon plasma, which are each estimated to require a timescale of the order of 10-22 s. Therefore, unlike the other quarks, the top quark decays before such processes can occur. It can also decay within the quark-gluon plasma itself. This decay produces other quarks that experience intense interaction with the quark-gluon plasma, as shown in Figure 2.
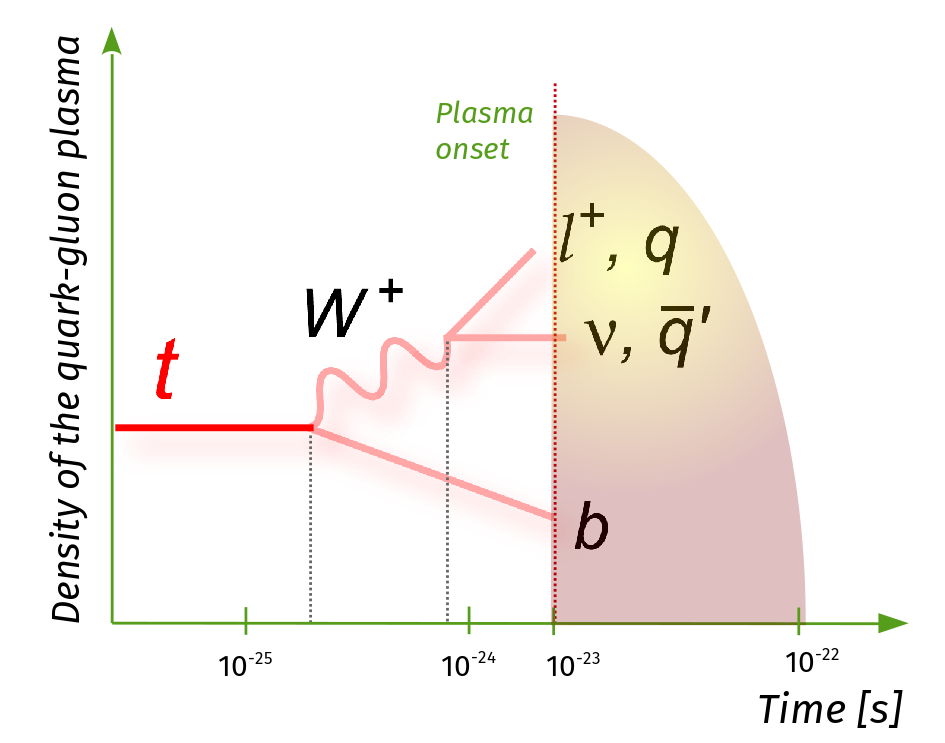
Figure 2: Top quarks almost always decay into a b quark and W boson; the latter further decays into leptons or quarks that can be detected and form the so-called “final state”. The sketch illustrates the process of the top quark decaying to other particles, and the average decay times of each particle are indicated on the x-axis. The quark-gluon plasma density evolution (y-axis) is illustrated as a function of time.
From the above reasons, top quarks can provide insights into the highest energy collisions. They also enable us to study how the quarks produced from top quark decay experience a “quench” in their energies through interactions with quark-gluon plasma. However, such studies are easier said than done. Heavy-ion collisions produce a huge number of particles, putting even the very advanced particle reconstruction algorithms of CMS under stress. Indeed, CMS is a multipurpose experiment, mostly optimized for high-energy proton-proton collisions. Therefore it would be unfair to expect it to be equally performant using heavy ion data but, to interpret this, the CMS experiment uses re-optimized software.
It took years to build confidence that it was even possible for the CMS experiment to find top quarks in lead-lead collisions. A crucial milestone was the first observation of top quark production in proton-lead collisions using data taken in 2016 [Phys. Rev. Lett. 119, 242001 (2017), https://arxiv.org/abs/1709.07411]. As a lead atom is composed of 208 "nucleons" (protons or neutrons), a proton-lead collision provides 208 times more opportunities for quarks and gluons to collide, with respect to a proton-proton collision. Consequently, this results in a higher number of particles in the final state. But the problem of top quark identification in lead-lead collisions was still a tougher nut to crack: although the probability to produce a top quark is a factor of (208)x(208), or approximately 40,000, larger in a Pb-Pb collision than in a p-p one, the corresponding backgrounds are also similarly enhanced. Most importantly, the amount of data collected in a typical Pb-Pb run is orders of magnitude smaller than in p-p collisions, and the energies of the collisions between their elementary components are also smaller, leading to much fewer signal events.
Figure 3: A lead-lead collision event interpreted as containing the decay products of a top quark and a top antiquark.
Figure 3 shows an example of how a top quark event is produced in a busy environment after a head-on, lead-lead collision. This event was recorded by the CMS experiment in late 2018. The number of extra particles is overwhelming, but there are recognisable features that indicate top quark production: a very energetic electron (green) leaving a large deposit in the electromagnetic calorimeter, a very energetic muon detected by the muon detectors (red), and two very energetic hadronic jets (orange) containing signs of originating from the hadronisation of b quarks (hence passing a so-called “b tagging” algorithm).
Being produced in almost 100% of the top quark decays, b quarks are a crucial signature of top quark presence. On the other hand, as mentioned above, b quarks interact with quark-gluon plasma, potentially biasing the results. Thus, the quark-gluon plasma itself must be better understood before such results can be correctly interpreted.
To achieve this, two complementary analyses were performed. One was based entirely on the features of the two leptons observed in the event, intentionally ignoring any information related to the hadronic jets in order to stay away from such subtleties. However in the second analysis, the presence of b-tagged jets was also exploited, with extra uncertainties considered in the final fit to the data. In both cases two light, charged leptons (i.e., electrons or muons) were selected, with charges opposite in sign. Also in both cases, a machine learning algorithm (a boosted decision tree, or BDT) was used to distinguish between events that were more likely to be the desired top quark production process, known as the signal process, and those that are less likely to be the desired process, known as background processes.
Events containing an electron and a muon in their final states were grouped depending on the number of b-tagged jets they contained (0, 1 or 2). Then, for the events in each group, results from the machine learning algorithm were compared to the best-fit signal and background expectation. This is shown in Figure 4.
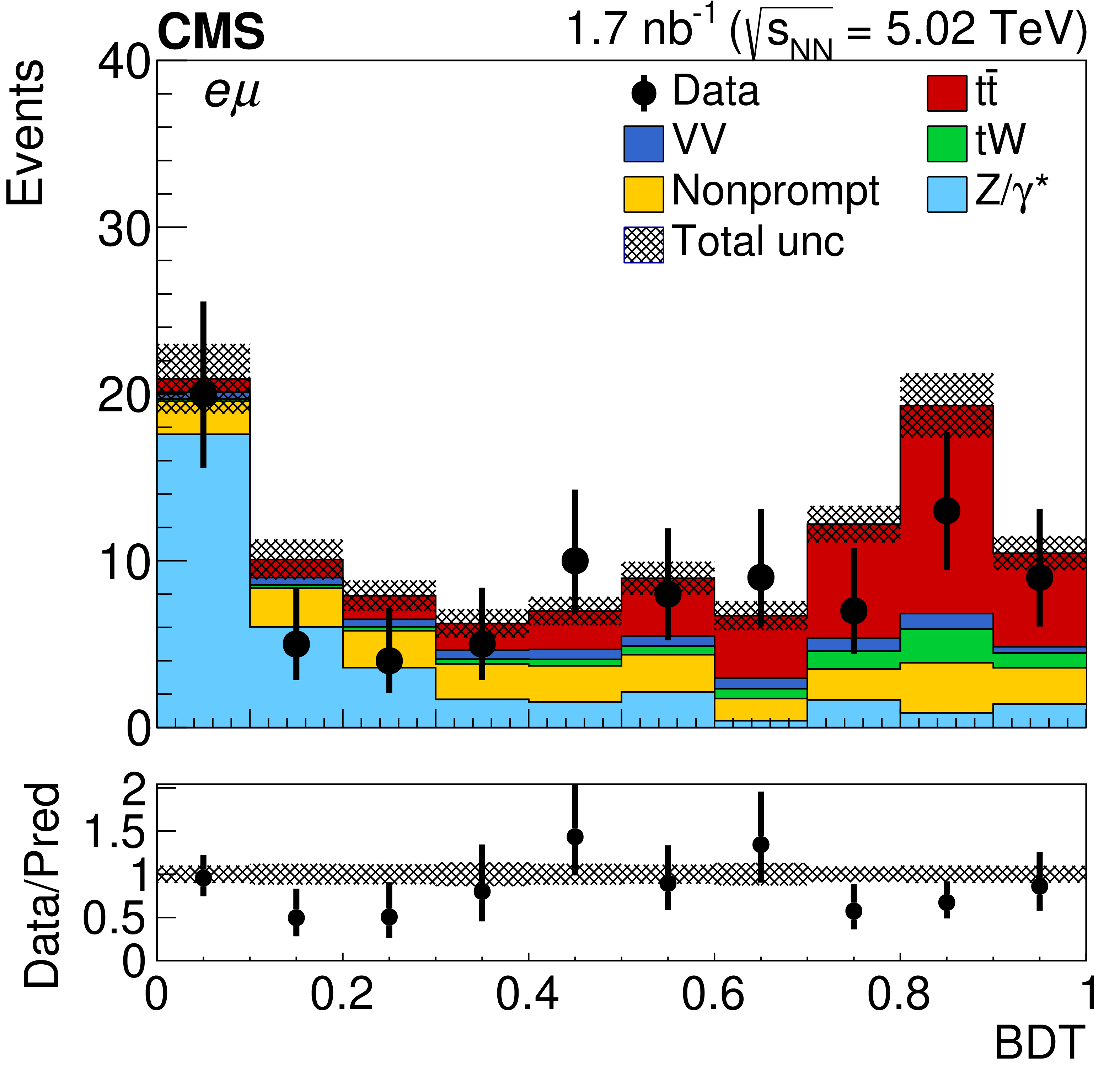
Figure 4: The number of events in data, the estimated numbers of events in the top quark pair signal and background processes and the total uncertainty.
The two analyses yield results consistent with each other and with theory expectations. Results are also consistent with extrapolations from previous measurements of the tt̄ cross section in proton-proton collisions, at the same center-of-mass energy per nucleon (see Figure 5). If no top quarks were produced in lead-lead collisions, there would be a probability of 0.003% (or four sigma) that the signal would arise from a background fluctuation.
Figure 5: Results of the cross section measurements from the two alternative analyses (with and without exploiting the b-tagged jets). To compare the new results, a reference measurement from proton-proton collisions was corrected for the number of protons and neutrons in the lead nucleus. The expectation from theory calculations is also shown.
This new measurement is not the end of the story, but is rather the beginning. With more data and ingenuity, CMS members could embark on an even more challenging decay channel, in which one W boson decays into two leptons (as in Figure 2) and the other into two quarks, which in turn decay into hadrons. Reducing the number of background events in that channel would be more difficult, but it would pay off in terms of using LHC data to increase our understanding of the interactions between quarks and the quark-gluon plasma. For example, deviations in the measured invariant mass distribution of the two quarks from the well-known W boson mass could be determined, which could be used to indirectly measure the effect of the quark-gluon plasma on the propagation of quarks. Such a measurement would complement already established techniques. With even more data, this measurement could be performed in different ranges of the top quark momentum. This is, in turn, correlated with the time it takes to go from the formation of top quarks to the presence of stable hadrons. This could provide physicists a unique window on two, big open questions in fundamental physics: how much time does the quark-gluon plasma take to form, and how long does it take to cool down?
Read more about these results:
- CMS Paper "Evidence for top quark production in nucleus-nucleus collisions"
- All CMS physics briefings
- All CMS journal publications
- All CMS preliminary results
- All CMS results