On the hunt for a rule-breaking heavy boson

By CMS Collaboration

The CMS Collaboration probes decays of the Z boson which would defy our expectations of lepton behavior

How strict are Nature's conservation laws governing the interactions among elementary particles? Physicists once assumed, based on experience with the electromagnetic interaction, that parity would always be conserved. Then, a 1957 experiment found that when a nucleus undergoes beta decay, which occurs via the weak interaction, the process distinguishes between the left- and right-handed electrons. This startling finding implied that parity is in fact not conserved in the weak interactions. Ever since, researchers have been motivated to probe various conservation laws.

The W boson is a quantum particle associated with weak interactions. It is able to change a particle’s flavor and electric charge, as occurs in nuclear beta decay. Accordingly, the W boson can transform a neutrino into an electron or muon matching its flavor. In 1973, results from the Gargamelle bubble chamber concluded that a neutrino can also scatter and continue unchanged, which implied the existence of the Z boson, and validated the electroweak interaction. Observations in 1983 of direct production of the W and Z bosons established their masses at 81 and 92 GeV, respectively.

Inverse processes to the scattering of neutrinos occur as well, such as decays of the Z boson to charged lepton pairs: Z→e^-e⁺, Z→μ^-μ⁺, and Z→τ^-τ⁺. Could the Z boson decay to charged lepton pairs of mixed flavor, i.e, Z→e^-μ⁺, Z→e^-τ⁺, or Z→μ^-τ⁺? This is the question addressed by this CMS study. These LFV processes are not expected to occur according to the standard model (SM) of particle physics.

Proposed extensions of the SM to address some of its shortcomings include ones that contain a heavier weak boson, referred to as Z'. In some models, LFV decays of the Z' are allowed and, through mixing with the SM Z boson, LFV decays of the Z boson could occur as well.

This new analysis from CMS considers decays of the SM Z boson to all of the LFV combinations of lepton pairs, e^-μ⁺, e^-τ⁺ and μ^-τ⁺, and further extends the search in the e^-μ⁺ channel to include a possible heavier Z' or other neutral boson.

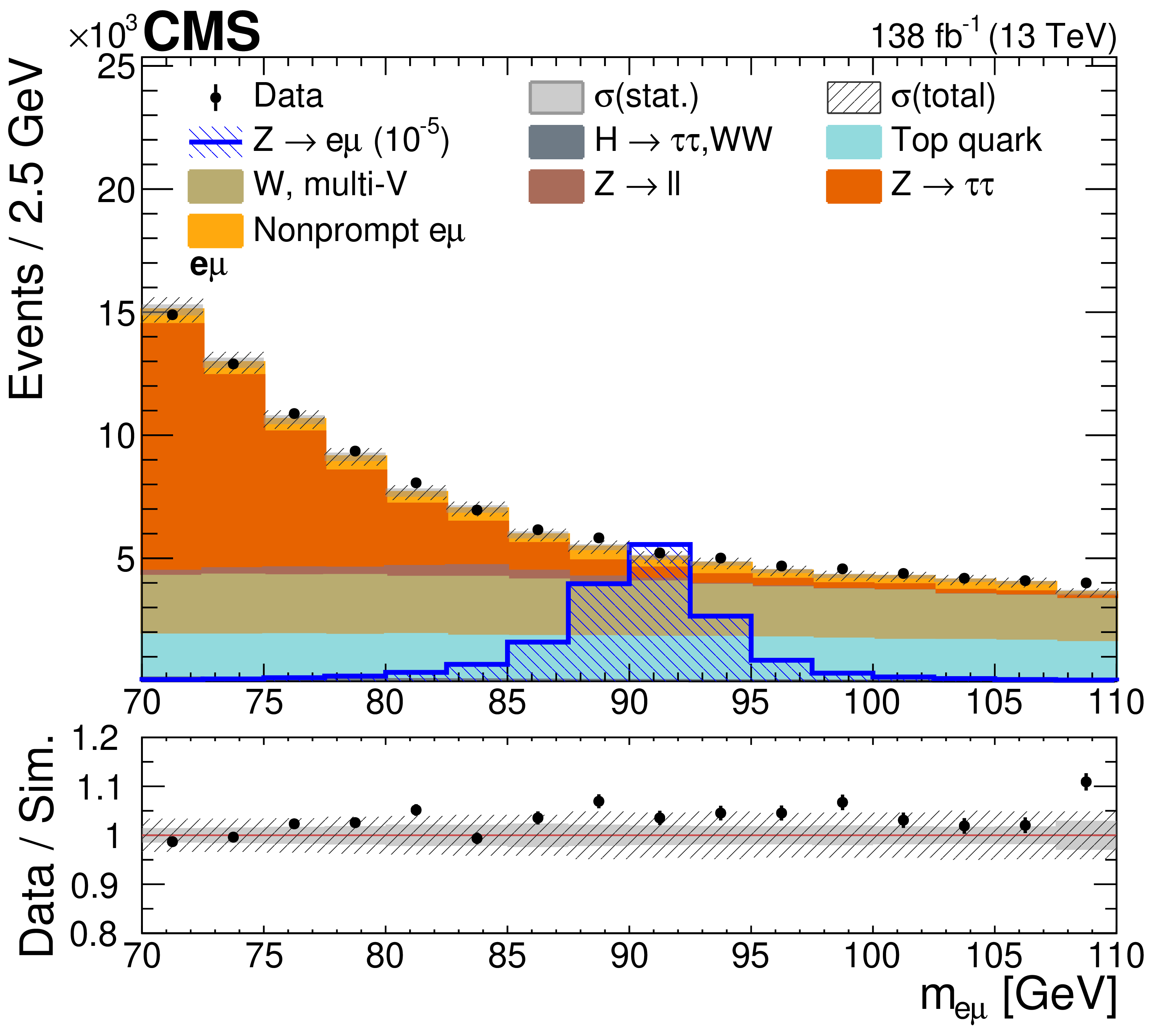
Figure 1: Invariant mass of the eμ system for data (points with error bars) and simulated background (stacked filled histograms). The hatched histogram shows a hypothetical Z→eμ signal. The lower panel shows the ratio of the data to simulated yields, with the uncertainty of the simulated yield indicated by the gray band.

For the decay Z→e⁻μ⁺, the invariant mass of the dilepton system would exhibit a narrow peak at the mass of the Z boson, as illustrated in Fig. 1. The figure shows the smoothy-falling distribution arising from the cumulative yields of the various SM background processes, with an overlay of the simulated signal. The selection of events makes use of a multivariate discriminant, specifically a boosted decision tree, which combines the most discriminating properties of the events into a single variable.

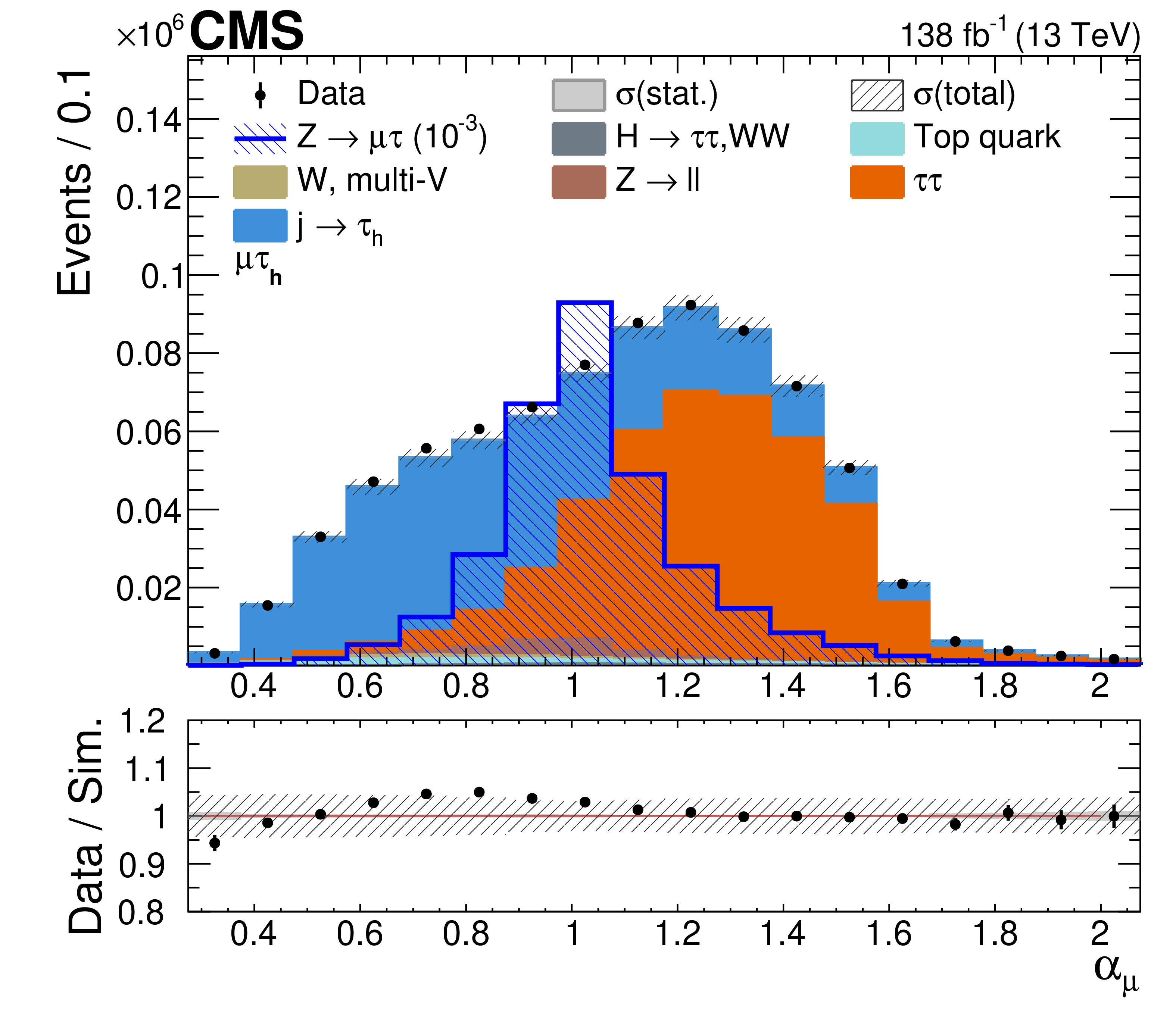
Figure 2: Distributions of μτ_h signal and estimated backgrounds in α_μ for the data (black markers with error bars) and the simulated backgrounds (filled stacked histograms). The lower panel shows the ratio of the data to simulated yields, with the uncertainty of the simulated yield indicated by the gray band.

For the decay channels involving τ leptons, the analysis is more challenging. This is because the τ lepton is unstable, decaying to final states with one or two unobservable neutrinos in addition to the detected daughters. Optimal use of the available kinematic information leads to the introduction of a variable α, whose distribution is shown in Fig. 2 for the μ⁻τ⁺ channel.

No excess of events above the SM predictions is observed, and so the results are used to set limits on the branching fractions of LFV decays. We conclude that, if the LFV decays of the Z boson occur at all, they have very small branching fractions. This analysis sets the most stringent limits on the Z′ → eμ process within the scanned mass range and represents an improvement of more than an order of magnitude in sensitivity to a Z′ signal in the low mass region.

Read more about these results: