It is the dream of all particle physicists to find a new particle or to reveal a new fundamental force. In 2012 this dream came true when the big CERN experiments ATLAS and CMS discovered the Higgs particle, predicted by theorists decades ago. Other examples of successful searches are the W and Z bosons, mediating weak forces, which were detected first in the 1980s at CERN. These massive particles had been forecasted by theory. In both these cases, the properties of the particles were predicted precisely by the Standard Model, so physicists knew exactly for what objects to look. But what happens when one does not know what the properties of the particles could be? To be sure dedicated searches miss no new particles, CMS physicists also perform a general search.
This dedicated search method can be translated into daily life: you lost your keyring and search for it in your kitchen - you expect it to be there, and you know what it looks like exactly. But can your kitchen contain something completely new, where there is no idea at all what it could be? In the analogy, maybe you suspect that a friend visited your kitchen in your absence, and possibly they hid a surprise present. To investigate this, you could systematically check each cupboard and all corners if anything is different from what you expect. Obviously, that method assumes that you know your kitchen very well – and searching would be almost impossible to try in a place that you do not know in great detail already.
In particle physics, we try to do the same, and the Standard Model is our kitchen. By now, theoretical calculations based on the Standard Model can accurately predict most effects of the electromagnetic, weak, and strong forces in high-energy interactions of the known elementary particles. This foundation is the reason why the Standard Model of particle physics is considered so successful. Already its name implies that it is a very solid theory. It has become the standard to describe everything particles can do, that is, how they decay and interact. In particular, the Standard Model can predict extremely precisely what can happen when two protons are smashed into each other with high energy, as is done with the Large Hadron Collider, the LHC. And the CMS detector has already recorded billions of such collision events. It then becomes possible to compare theoretical prediction and all experimental data - and search for any deviation that might indicate new physics! Such a Model Unspecific Search in CMS has been given the name MUSiC.
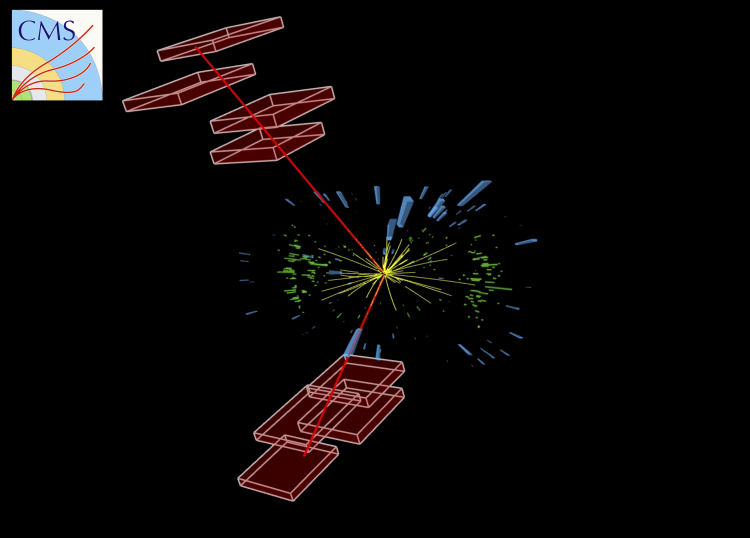
MUSiC starts by counting which (known) high energy particles are produced in one collision event, for example, muons or high energy photons, or bundles of hadrons, which are called jets. Fig. 1 shows a CMS event display resulting from a single proton-proton collision. In this collision, two muons can be observed, shown as long red lines originating in the centre, at the proton-proton collision point. The muons traverse several muon detectors, the outer red boxes in the image. The green and blue symbols indicate low energy particles, which are not considered. This approach is appropriate in high energy collisions, where likely signatures originate from decays of new undiscovered particles, and those are mostly predicted to be massive. The collision shown in Figure 1 is called a 'two muon' event as it contains two muons. Similarly, it is possible to define hundreds of classes, like 'two electrons plus one photon' or 'one muon plus three jets'. The number of possible combinations is huge, any number of muons, electrons, photons, or jets, can be considered, and this is why the MUSiC method is very complementary to the searches for specific new particles that are also part of the CMS programme.
The first step in the analysis is to compare the number of events in each class to the Standard Model prediction. This comparison is shown in graphical form in Figure 2, for some of the particle combinations, in this case, those with at least two electrons plus other particles. The colours indicate the different Standard Model contributions, for example in yellow, top pair production, with subsequent decay, yielding two electrons. The agreement between measurement and theory is excellent within the uncertainties! This procedure is repeated by adding other objects, for example, jets that can also come from b quarks. In each of the selections, the event yield is predicted by the Standard Model and compared to the data. As the predictions agree within the uncertainties, there is no hint for new physics.
 Figure 2: The number of expected and observed events in collisions with two electrons with- or without- additional jets, including the possibility that the jets come from b quarks. The multi-coloured distribution contains all Standard Model production mechanisms that can create two muons. The data (black points) agree with the Standard Model prediction, including its uncertainties.
Figure 2: The number of expected and observed events in collisions with two electrons with- or without- additional jets, including the possibility that the jets come from b quarks. The multi-coloured distribution contains all Standard Model production mechanisms that can create two muons. The data (black points) agree with the Standard Model prediction, including its uncertainties.
But counting events with leptons and jets is only looking at the surface; it is possible to also look at all these event classes in detail, by studying important kinematical distributions. To do so, the energy and flight direction for each of the identified objects are measured. An example of one of the kinematical variables is the total invariant mass, calculated from all the particles in one event. This invariant mass variable is a measure of how energetic the collision was. Figure 3 shows the mass distribution for one event class, 'two muons'. The event in Figure 1 is part of this sample. When investigating the invariant mass distribution, the overall agreement between theory (histogram) and data (points) is excellent. To confirm, a search algorithm automatically looks for inconsistencies in these distributions with the most significant deviation between CMS data and theoretical prediction. This 'region of interest' is marked by two vertical dashed red lines. Note that adding new physics to the Standard Model can make the predicted number of events go either up or down. In this case, the Standard Model predicts slightly more events there than the data shows, as can best be seen in the ratio between data and Standard Model Monte Carlo prediction at the bottom of Figure 3. Further statistical analysis also reveals that this most substantial difference is still not statistically significant.
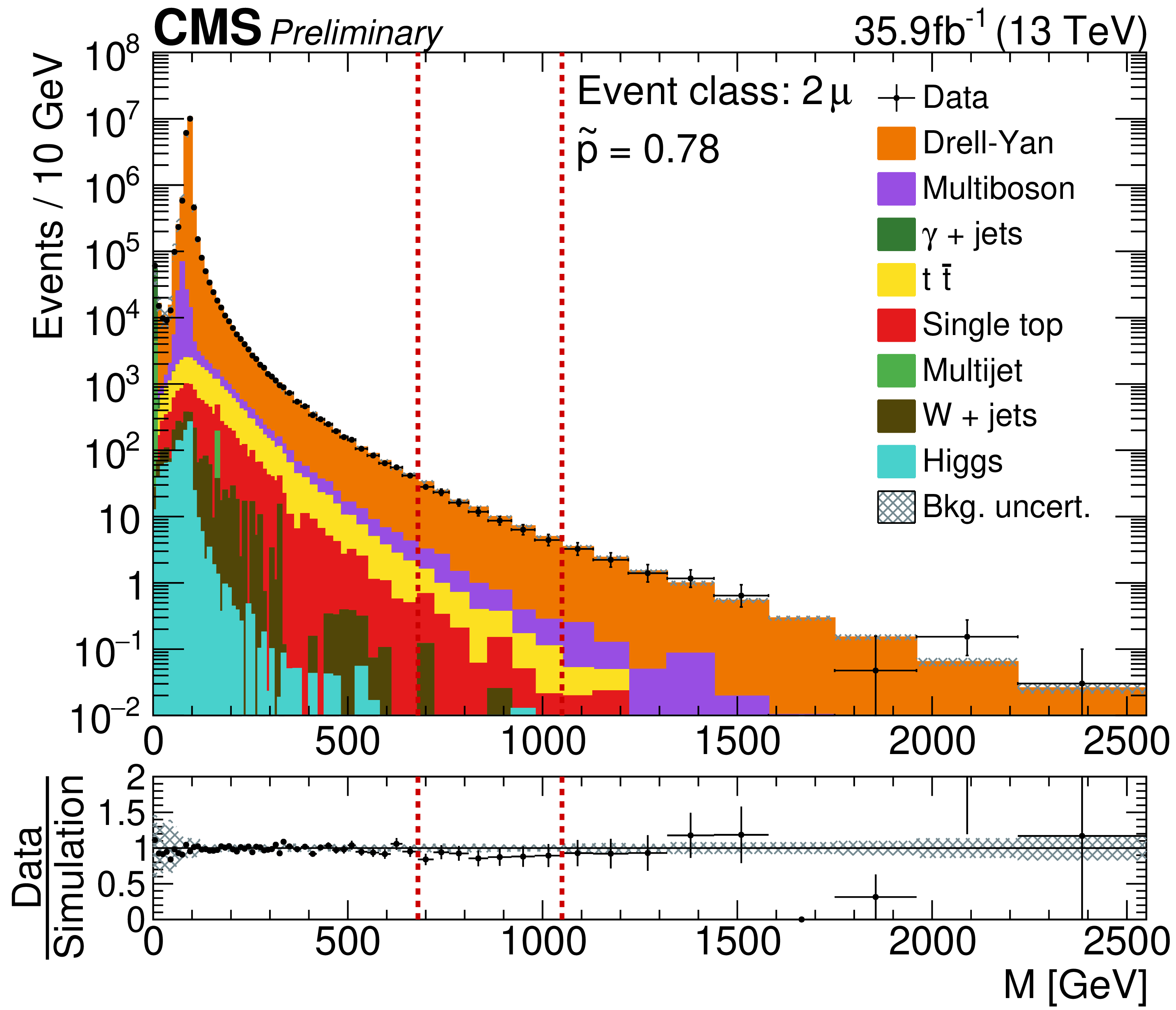 Figure 3: The two-muon invariant mass distribution created observed in the 2016 CMS dataset. The multi-coloured distribution contains all Standard Model production mechanisms that can create two muons. The data (black points) agrees with the Standard Model prediction. The bottom part of the plot shows the data divided by the Standard Model prediction. In the area between the red lines, the data is slightly smaller than the prediction by the Standard Model, but not in a significant way.
Figure 3: The two-muon invariant mass distribution created observed in the 2016 CMS dataset. The multi-coloured distribution contains all Standard Model production mechanisms that can create two muons. The data (black points) agrees with the Standard Model prediction. The bottom part of the plot shows the data divided by the Standard Model prediction. In the area between the red lines, the data is slightly smaller than the prediction by the Standard Model, but not in a significant way.
In this manner, the CMS collaboration has investigated numerous distributions from the 2016 dataset with the MUSiC method. In some cases, the difference between theory and experiment is a bit bigger than in Figure 3. Still, altogether the MUSiC analysis found no substantial deviations, and so far CMS physicists do not see a clear signal of new physics.
This new result uses only the data collected in 2016; there is a lot more data available from the LHC Run 2 that ran up to 2018. In the next years, the LHC will produce many more proton-proton collisions, and the MUSiC algorithm is ready to find whatever nature will provide.
Read more about these results:
- CMS Paper "MUSiC, a model unspecific search for new physics, in pp collisions at sqrt(s)=13 TeV"
- All CMS physics briefings
- All CMS journal publications
- All CMS preliminary results
- All CMS results
- Log in to post comments

