Neutron stars, ultra-cold atomic gasses, and the quark-gluon plasma… You may find them totally unrelated but, surprisingly enough, they share a common feature: a fluid-like state of matter containing strongly interacting particles! An insight into the behavior of any of these almost perfect liquids will be the key in understanding Nature at scales that are orders of magnitudes apart. For example, we may ask about the transport of matter in such environments. The answer makes us think of “sound”: a longitudinal wave that travels through a medium while producing compressions and rarefactions of matter in the direction of its movement. The speed of sound depends on the medium’s properties, such as the fluid’s density or viscosity, so that it can be used as a probe of fluid-like matter.

Heavy ion collisions at the very-high LHC energies deposit a gigantic amount of energy in a very small volume, similar to that of an atomic nucleus. The quarks and gluons produced in the collision can freely roam within this volume, composing an extremely hot medium, the so-called quark-gluon plasma (QGP). The collective dynamics and macroscopic properties of this fluid-like matter are well described by the principles of nearly-ideal relativistic hydrodynamics. The speed of sound in this environment can be evaluated from the way the medium pressure changes in response to variations in the energy density.

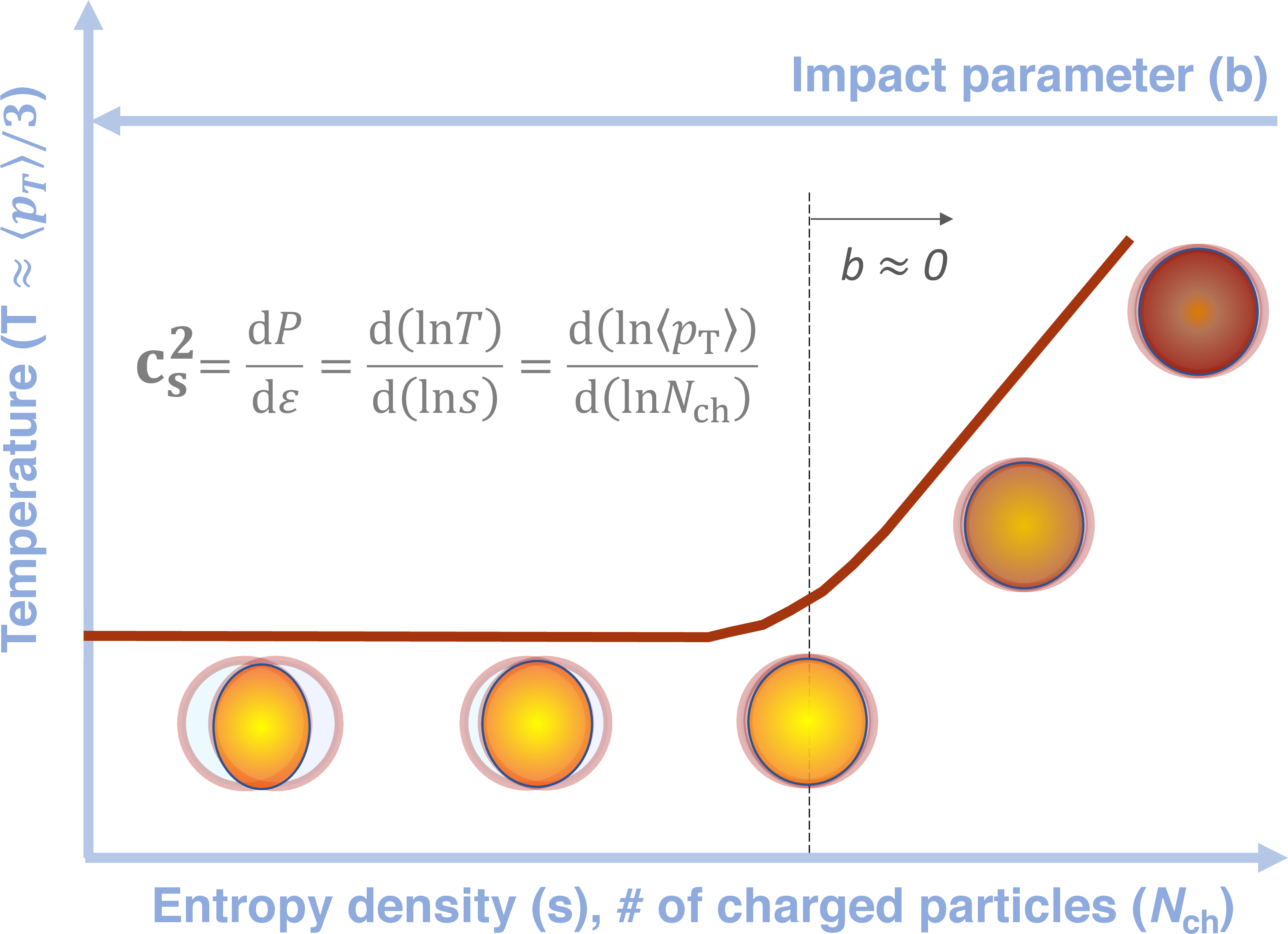
Figure 1: Conceptual representation of temperature vs. entropy density from mid-central to ultra-central heavy ion collisions.

Heavy ion collisions are characterized by their impact parameter, the distance between the centers of the two nuclei in the plane transverse to the beam line. Collisions with a smaller impact parameter have a bigger overlap area, producing QGP fluids with a larger amount of deposited energy, while maintaining a nearly constant energy density and/or temperature. This trend reaches a limit for head-on collisions, where the impact parameter approaches zero, because the medium size cannot be bigger than the geometrical volume of the colliding nuclei. However, the deposited energy can still grow, because of fluctuations. In thermodynamics, the energy (or heat content) of a medium is related to its temperature and entropy. Figure 1 illustrate the relation between the temperature, the impact parameter, and the entropy density. Using fundamental rules of thermodynamics, the speed of the sound can be evaluated from the rate of temperature change in response to entropy variations. Entropy is a measure of disorder in the system and depends on the number of states that the system constituents can take. In heavy-ion collisions this can be inferred from the number of the emitted charged particles, N_ch. The temperature relates to the average transverse momentum of the emitted particles, <p_T>.

Figure 2: The average transverse momentum of charged particles, $<p_T$, as a function of the charged-particle multiplicity, $N_{\text{ch}}$. Both $p_T$ and $N_{\text{ch}}$ are normalized by their values in highly central events. Bars and the red band correspond to statistical and systematic uncertainties, respectively. Hydrodynamic simulations from two different models are also shown for comparison.

Physicists in CMS have measured, for the first time, how N_ch varies as a function of <p_T> in the most central heavy ion collisions. Figure 2 shows the measurement, compared with predictions of two theory models. The squared speed of the sound (in units of the speed of light) is determined to be (c_s/c)² = 0.241 ± 0.002 (stat) ± 0.016 (syst) whereas the effective temperature of the QGP system is estimated to be T_eff = 219 ± 8 (syst) MeV.

Figure 3: The speed of sound, , as a function of the effective temperature, $T_{\text{eff}}$, with the CMS data point obtained from ultra-central heavy ion collision data. The size of the red box indicates systematic uncertainties of and $T_{\text{eff}}$, while statistical uncertainties are smaller than the marker size. The measurement is compared with a previous result (green box), the outcome of a simulation (blue box), and the prediction from lattice QCD calculations (dashed curve). The dashed line at the value of 1/3 corresponds to the upper limit for noninteracting, massless gas (``ideal gas'') systems.

Figure 3 shows how the squared speed of the sound varies with T_eff, in the measurement and in three different theory calculations. The CMS measurement represents the most precise result to date.

Read more about these results:

• CMS Physics Analysis Summary "Extracting the speed of sound in the strongly interacting matter created in ultrarelativistic lead-lead collisions at the LHC"

• @CMSExperiment on social media: LinkedIn - facebook - twitter - instagram

• All CMS physics briefings

• All CMS publications

• All CMS preliminary results

• Search all CMS results

• Do you like these briefings and want to get an email notification when there is a new one? Subscribe here